Hagen–Poiseuille Flow Rate Calculator - Calculate flow rate from pressure

Hagen–Poiseuille flow rate calculator

Starting Pressure (p₁):

Ending Pressure (p₂):

Pipe Diameter (D):

Dynamic Viscosity (μ):

Length of Pipe (L):

Unit	Flow Rate (Q)
m³/s
m³/min
m³/h
L/s
L/min
L/h
cm³/s
cm³/min
cm³/h
mm³/s
mm³/min
mm³/h
ft³/s
ft³/min
ft³/h
in³/s
in³/min
in³/h
yd³/s
yd³/min
yd³/h
gal/s
gal/min
gal/h

How to Calculate Flow Rate Using Hagen–Poiseuille Equation

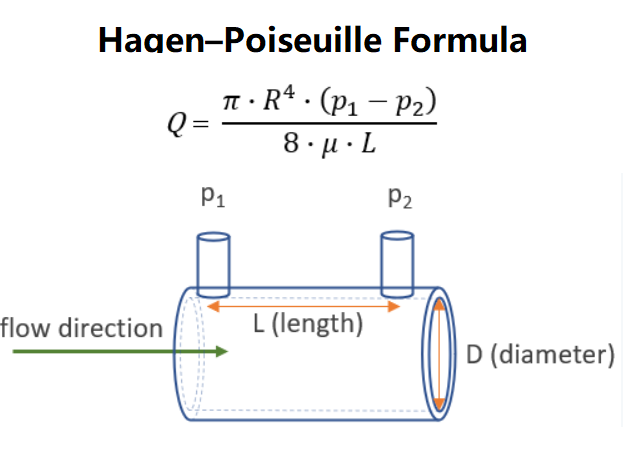
The Hagen–Poiseuille equation is used to calculate the flow rate of a fluid through a pipe, taking into account the viscosity of the fluid, the length of the pipe, the pipe radius, and the pressure difference between the two ends:

$$ Q = \frac{\pi \times (p_1 - p_2) \times R^4}{8 \times \mu \times L} $$

Where:

Q: Flow rate (m³/s)
p₁ - p₂ (ΔP): Pressure difference (Pa)
R: Radius of the pipe (m)
μ: Dynamic viscosity of the fluid (Pa·s)
L: Length of the pipe (m)
π: Pi constant (3.14159...)

Use the form above to input the values, and the calculator will provide the flow rate through the pipe.

Hagen-Poiseuille's Law

Definition & Statement

The Hagen-Poiseuille Law, also known as Poiseuille's law or the Hagen-Poiseuille equation, is an important principle in fluid dynamics. It describes the pressure loss in a fluid flowing through a narrow pipe (e.g., blood vessels, urinary catheters, or cooling channels in plastic injection molds). Specifically, the pressure loss is directly proportional to the product of the volume flow rate, dynamic viscosity, and pipe length, and inversely proportional to the fourth power of the pipe radius.

Formula Expression

The Hagen-Poiseuille law can be expressed as:

ΔP = (8πμL) / (R^4) × Q

Where:

ΔP: Pressure loss.
μ: Dynamic viscosity of the fluid.
L: Length of the pipe.
R: Radius of the pipe (Note: the formula has the inverse of the fourth power of the radius, not the diameter, as the diameter is twice the radius).
Q: Volume flow rate, the volume of fluid passing through the pipe per unit of time.

Applicable Conditions

The Hagen-Poiseuille law is applicable under the following conditions for the fluid:

Incompressible fluid: The fluid density remains constant during flow.
Newtonian fluid: The fluid's viscosity does not change with flow velocity.
Laminar flow: The fluid flow must be laminar (not turbulent), meaning that fluid layers flow smoothly with minimal disruption between them. The pipe diameter should not be too large to ensure laminar flow stability.
Length greater than diameter: The length of the pipe should be greater than its diameter for accurate application of the law.

Practical Applications

The Hagen-Poiseuille law has wide applications in various fields, including but not limited to:

Physiology: In hemodynamics and blood rheology, the law is used to describe the flow of blood through blood vessels.
Engineering: In plastic injection molds, the law helps predict pressure loss in the cooling channels of the mold.
Civil Engineering: In hydraulic studies, it is used to analyze water flow in pipes.

Important Notes

Note: The Hagen-Poiseuille law may not be accurate for very short tubes, low-viscosity fluids, wide tubes, or high flow velocities, as these conditions can lead to turbulent flow, which causes actual pressure loss to be higher than predicted by the law.