Pump Affinity Laws Calculator - Changing Impeller Diameter

Calculate:

Initial Flow Capacity (\( q_1 \)):

Initial Head (\( dp_1 \)):

Initial Power Consumption (\( P_1 \)):

Initial Impeller Diameter (\( d_1 \)):

Final Impeller Diameter (\( d_2 \)):

Final Value in Brake Horsepower (BHP):

Final Value in Kilowatts (kW):

Final Value in Horsepower (hp):

1. What is the Pump Affinity Laws Calculator for Changing Impeller Diameter?

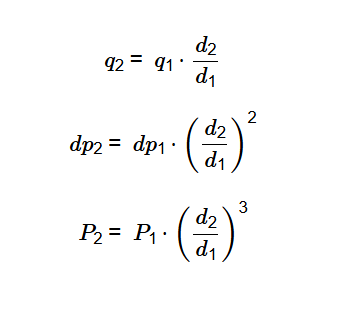
Definition: This calculator applies the Pump Affinity Laws to compute the final flow capacity (\( q_2 \)), final head (\( dp_2 \)), or final power consumption (\( P_2 \)) when the impeller diameter changes, assuming a constant pump speed.

Purpose: It is used in mechanical engineering to predict the performance changes in a pump system due to impeller diameter variations, aiding in design, optimization, and operational adjustments.

2. How Does the Calculator Work?

The calculator uses the following relationships:

\[ q_2 = q_1 \cdot \frac{d_2}{d_1} \] \[ dp_2 = dp_1 \cdot \left( \frac{d_2}{d_1} \right)^2 \] \[ P_2 = P_1 \cdot \left( \frac{d_2}{d_1} \right)^3 \]

Where:

\( q_2 \) — Final flow capacity (in various units)
\( q_1 \) — Initial flow capacity
\( dp_2 \) — Final head (in various units)
\( dp_1 \) — Initial head
\( P_2 \) — Final power consumption (in various units)
\( P_1 \) — Initial power consumption
\( d_2 \) — Final impeller diameter
\( d_1 \) — Initial impeller diameter

Explanation: Select the parameter to calculate (final flow, final head, or final power), enter the corresponding initial value (flow, head, or power), initial impeller diameter, and final impeller diameter in the chosen units. The initial value is converted to its base unit (gpm for flow, ft for head, BHP for power), and the diameters are converted to inches. The final value is computed based on the selected affinity law. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( q_1 = 100 \, \text{gpm} \), \( d_1 = 8 \, \text{in} \), \( d_2 = 6 \, \text{in} \)), the calculated final flow \( q_2 \) is approximately 75.00000 gpm.

3. Importance of Pump Affinity Laws Calculation for Changing Impeller Diameter

Details: Calculating the changes in flow, head, and power consumption using the Pump Affinity Laws for impeller diameter changes is essential for adjusting pump performance, optimizing energy use, and ensuring system efficiency when modifying impeller sizes.

FAQ

How do I calculate the final flow, head, or power for an impeller diameter change?

Select the parameter to calculate (flow, head, or power), enter the corresponding initial value (flow, head, or power), initial impeller diameter, and final impeller diameter in the chosen units. Use the formulas \( q_2 = q_1 \cdot \frac{d_2}{d_1} \), \( dp_2 = dp_1 \cdot \left( \frac{d_2}{d_1} \right)^2 \), or \( P_2 = P_1 \cdot \left( \frac{d_2}{d_1} \right)^3 \) based on your selection.

What do the Pump Affinity Laws for impeller diameter changes represent?

The Pump Affinity Laws describe how flow, head, and power consumption change with impeller diameter, assuming a constant pump speed, providing a method to predict performance adjustments.

What are the formulas for the Pump Affinity Laws when changing impeller diameter?

The formulas are: \( q_2 = q_1 \cdot \frac{d_2}{d_1} \) for flow, \( dp_2 = dp_1 \cdot \left( \frac{d_2}{d_1} \right)^2 \) for head, and \( P_2 = P_1 \cdot \left( \frac{d_2}{d_1} \right)^3 \) for power, where \( d_1 \) and \( d_2 \) are the initial and final impeller diameters.

Can I use different units for flow, head, power, and impeller diameter?

Yes, the calculator supports multiple units for flow (gpm, L/s, m³/h), head (ft, m), power (BHP, kW, hp), and impeller diameter (in, cm, m). All inputs are converted to their base units for the calculation.

What happens if I enter zero for the initial or final impeller diameter?

Entering zero for the initial impeller diameter (\( d_1 \)) or final impeller diameter (\( d_2 \)) will result in the calculation not being performed, as the formula involves a diameter ratio. Both diameters must be greater than zero for a valid result.

Favorite